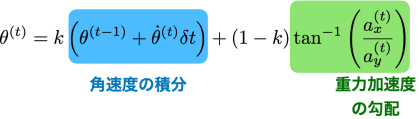モーションセンサの姿勢推定
モーションセンサ（以後，MS）は３次元の姿勢推定を行い，オフラインでは単位クォータニオンをCSVファイルに出力し，オイラー角にも変換できます．オンラインで図１のようなアプリで３D表示したり，クォータニオンを出力することもできます（独自アプリケーション開発には、別途、SDKが必要となります）．
ここで述べる「３次元の姿勢（角度）」とは，剛体（変形しない形のある物体）にXYZの直交する座標系を定義して，その座標軸の各方向を示しています．
３次元の姿勢表現の基本は回転行列で，その他に単位クォータニオン，オイラー角などがあります．詳細については「モーションセンサを使用した角度の算出方法 その1」「モーションセンサを使用した角度の算出方法 その2」をご参照ください．
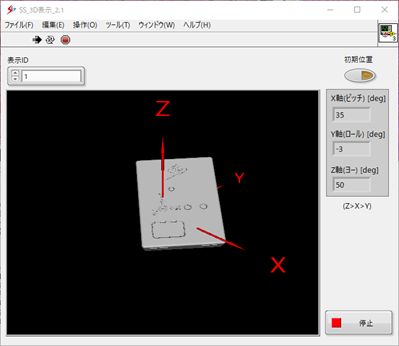
図１：姿勢角度表示アプリ
姿勢推定の概要
単位クォータニオンはMSに含まれるジャイロセンサによって計測される角速度を積分することで計算できます．計算式は「クォータニオンと角速度」をご参照ください．
なお，引用したページで述べているオイラーパラメータは，このページで述べている単位クォータニオンに相当しますが，このオイラーパラメータとは，大きさを１に正規化したクォータニオンを指しています（「クォータニオン3：ロドリゲスの式からクォータニオンへ」をご参照ください．なお，ページごとにクォータニオン関連の表現方法が，統一的ではないことお詫びいたします．順次，訂正いたします）．
さて，ジャイロセンサの角速度は高精度であるので，角速度を積分することで高精度な角度を算出できますが，後述するドリフトと呼ばれる誤差が発生します．また，初期値（初期角度，初期クォータニオン）も与える必要があります．
積分による角度計算とドリフト
図２：角速度の面積（正の領域はプラス，付の領域はマイナス）．この例では最終的にプラスマナス０で元に戻る．
角度計算の基本は，角速度の「積分」演算を通して行われます．
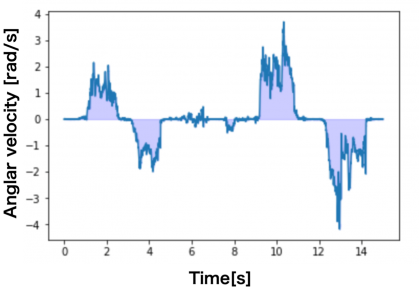
この「積分」とは幾何学的には角速度（Angular velocity）の曲線の面積を計算することに相当します（図２参照）．ただし，３次元の姿勢角度の場合は，速度と異なり「クォータニオンと角速度」に示したように，角度の計算が各xyz軸の角度と角速度が相互に依存するため，実際の計算手続きとしては積分する（Pythonではscipy.integrate.quad()など）というよりは，微分方程式を数値的に解くこと（Pythonではscipy.integrate.odeint() ）になります．
いずれにせよ，この面積の計算では誤差が逐次的に蓄積し，解が真値から時間経過とともに次第に少しづつずれていきます．
加速度から速度を計算する際も同様に面積の計算時に誤差が蓄積されますが，特にその速度をもう一度積分して（加速度の二階積分）位置を算出する際の誤差の蓄積はさらに激しく，とんでもない位置にずれてしまうのが通常です．
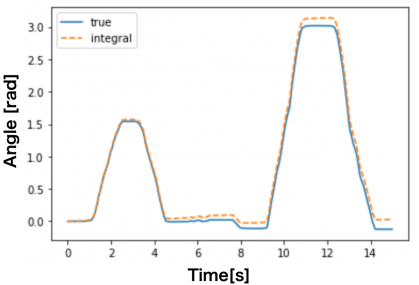
このような積分による誤差の性質はドリフトと呼ばれます．図３の例（わかりやすくするために意図的に誤差を大きくした例）ですと，２回ｚ軸回りに回転して戻すことを繰り返し，その時の角度変化の真値を青色の実線で示し，積分値をオレンジ色の破線で示しています．センサを水平状態から回転させて，もとの水平状態に戻しているので，最終的に角度が０に戻ってほしいのですが，15秒の時点で数度の角度変化を残しています．
図３：ドリフトの例（角速度の積分と真値の比較）
重力加速度ベクトルを使用した角度計算
ここでは，積分とは異なる角度の計算方法を取り上げ，その計算方法の基本的な考え方をご紹介します．
図４：モーションセンサに計測される重力加速度のxy成分
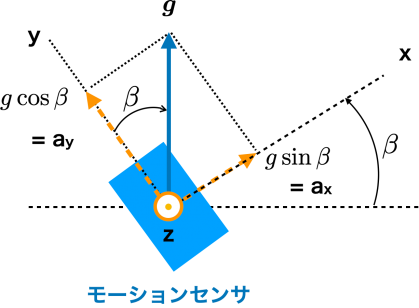
ここで取り上げる例では，回転軸を水平方向とする鉛直平面内の回転運動を想定し，MSのｚ軸を水平にしてこのｚ軸回りに回転させます．すると，重力加速度は鉛直方向に作用するので，傾けたMSの加速度計のx, y成分の両方に重力加速度の変化が計測され（図４参照），この加速度のaxとay成分の比を使用し，
の式によって，θ，すなわちMSの傾き（勾配，角度）を計算できます．
ここで，tan^(-1)は逆正接関数で，正接関数tan()の逆関数です．また，axとayは加速度計のx成分とy成分で，gは重力加速度を示しています．モーションセンサのxy成分には，重力加速度だけ検出されているとみなすことができる（近似できる）場合は，このように角度を，重力加速度を頼りとしたモーションセンサの傾き角度として計算できます．
この方法で計算される角度は，ジャイロセンサのようなドリフトによる誤差は発生しませんが，純粋な回転運動だけを与えて計測できることはまれなため，重力加速度以外の成分も含まることによって誤差を生じます．また，たとえMSを完全に静止させていとしても，加速度のaxとayの分解能や精度にも限界があり．誤差は発生します．
重力加速度以外にも地磁気ベクトルを頼りに補正する方法もありますが，基本的には絶対座標系に対して常に一定のベクトルを規範とし，センサに計測されるその勾配の成分から補正する点では同じです．ただし，重力加速度は「地面に対する傾き」を，地磁気は主として「方位角に対する傾き」を補正すると考えると良いでしょう．
プログラミング言語における逆正接関数 atan2()について
数学的には角度計算に逆正接関数tan^(-1)を使用しますが，多くのプログラミング言語では二引数を使用するatan2(±y, ±x)が準備されていますので，実際の角度計算にはatan2(±y, ±x)を利用します．
atan2(y, x)はtan()の逆関数（xとyから角度θを出力する関数）のPC言語などで使用できる組み込み関数で，atan2()は2引数，水平成分xと鉛直y成分をとり，引数の順番が(±y, ±x)となっていることに注意をしてください．また，Pythonではnumpy.arctan2(±y, ±x)という名前が異なっていたり，EXCELではATAN2(±X, ±Y)のように，順番がX,Yとなっているものもありますので，各自の計算環境でご確認ください．
このように，atan2(±y, ±x)は二つの引数をとることにより，値域が360度の範囲（４象限で計算．ただし，言語や使用する関数によって，値域は異なります）で符合付きで角度θを算出できますので，逆正接関数を利用した角度計算では，一引数のatan(y/x)ではなく，二引数のatan2(±y, ±x)を必ず使用しましょう．
また，角度を計算する逆関数として他にもacos()やasin()などがありますが，atan2()を使用しましょう．角度計算では二つのベクトルの内積を利用してacos()を使用する方が楽ですが，atan2()のほうが計算精度がよく，４象限の角度を計算できますので「atan2()を用いることが角度計算の基本」です．
重力加速度勾配による補正方法（単純化された相補フィルタの例）
図２にような時間の経過とともに蓄積されるドリフト誤差を補正するために，一般には，重力加速度や地磁気を補正のよりどころにして使うのが一般的な方法です．補正方法のアルゴリズムは多種多様に存在しますが，ここでは，その中でも単純化した１自由度の相補フィルタを例にとりあげ，補正方法の考え方の基本をご紹介します．
これまでご説明したように，ジャイロセンサはドリフト（低周波領域の特性が悪い）しますが，細かい波形はよく再現します（高周波領域の特性が良い）．一方，その反対に重力加速度による角度計算では，振動などの高周波ノイズに弱いのですが，ドリフトは発生しません．
そこで，ローパスフィルタで処理された加速度信号で計算した勾配角度と，反対にハイパスフィルタで処理されたジャイロセンサの角速度の積分で計算した角度との，重み付けされた和
式(１)：時刻(t)における角度θの推定式（単純化した相補フィルタの例）
を計算することで，角度を補正することができます．ここで，θは角度，kは重み係数（0から1），tは時間で，(t -1)は一つ前の計測時刻を表し，計測時間間隔をδtとします．
式（１）の右辺の第１項はジャイロセンサによる積分によるを意味し，第２項は重力加速度の勾配から算出した角度を示し，kの重み係数で配分しながら，第１項と第２項の和を計算しています．
一般にはkの値は大きく設定し（計測環境に依存しますが，実際には，約0.9以上の値を使用することが多い．適切な重み係数 k を選択するには，真値と比較することになる），波形はほぼジャイロセンサの積分で決まりますが，ドリフトによる誤差蓄積を第２項で補正していることになります．kの値は，どちらかというと加速度計から計測される重力加速度の比の精度に強く依存し，センサの性能もさることながら，計測環境（振動しがちな状況とか）に依存して決まる係数です．
３次元の補正推定の概要
ここで取り上げた例は，１自由度の角度補正法でしたが，３次元でもセンサ単体の角度推定は重力加速度を頼りに補正するのが基本で，他に地磁気センサと組合わせる場合もあります（当社の現在の姿勢推定アルゴリズムでは，地磁気センサを利用しておりません）．
また，３次元でも補正方法のアルゴリズムは多種多様ですが，「クォータニオンと角速度」の式をベースに積分演算を行うことを基本とすることは変わらず，大別すると補正方法としては，相補フィルタの他に，Kalman Filterや勾配フィルタなどの方法が存在します．たとえば，
https://ahrs.readthedocs.io/en/latest/filters.html
に取り上げられているように，計算環境Pythonで利用できる各種アルゴリズムが多くあることがわかります．収束速度などそれぞれ特徴はありますが，極論すると重力加速度を頼りに補正している点では大差がなく，またどの方法でも，常に正確な重力加速度を同定できるわけでもないため万能な方法は存在せず，スポーツなどのへの応用を考えると，悪く述べればそれほど大きな違いがないとも言えます．注意点としてはスポーツのような激しい運動を行っている際には，加速度信号には重力加速度以外の成分の多く含むため，どの方法でも推定精度は悪くなります．単純な積分のほうが精度が良くなることも十分に起こりえます．
一般には，純粋にその場での回転運動を行っている場合の角度推定は良いですが，多くの場合では角度推定には限界があることをご理解ください．また，状況によって誤差発生要因が異なり，どの程度の誤差が生じるという数値を示すことも困難ですが，激しくMSが振動したりMSが動く場合などでは，20[deg]以上の角度誤差は容易に発生します．
なお，当社の姿勢推定アルゴリズムの詳細は公開しておりませんが，他のアルゴリズムと同様に，角速度の積分演算と重力加速度による補正によって計算をしております．
より正確な姿勢角度を推定するために
さらに，当社のセンサの角度推定をご利用になる際の注意点を以下にまとめます．
センサの出力を安定させるために「計測前に１５〜２０分電源を継続していれておく」（※ ここでは「暖機運転」と呼ぶことに済ます）ことを推奨しております．
そして，「暖機運転後に，センサのキャリブレーションを行って」ください（「モーションセンサのキャリブレーション」のページを準備中）．なお，キャリブレーションの値は，電源をオフにしますと反映されませんので，再度キャリブレーション行う必要がありますので，ご注意ください．キャリブレーションによってドリフトを低減させ，重力による角度補正をより正確にします．
角度の初期値（地面に対する勾配角度）は，MSの計測開始時の重力加速度の比から計算します．したがって，前述の計算アルゴリズムからも「姿勢角度の出力を利用する場合」は，「計測開始時にMSを静止させている」ことが重要です．
なお，姿勢推定の計算は比較的高いサンプリングレートで行うほうが正確です．そこで，ユーザが設定するアプリケーションのサンプリングレートとは独立に，当社の姿勢角度の計算はセンサのDSP内で常に1kHzで行っています．
方位角に関する注意点
前述のように姿勢角度のアルゴリズムに地磁気センサを使用していないため，「計測開始時のヨー角に相当する方位角をゼロとするように初期姿勢角度を定めています」．
地磁気による角度補正も原理的には可能ですが，補正は磁場環境に依存し，特に地磁気ベクトルを歪ませる原因である鉄が多いビルなどでは磁場が大きく歪み（歪み方も空間的に均一でない），地磁気情報を利用した角度補正によって，むしろ角度の推定精度を悪化させることが多いのが現実です．このような理由から，（2021.7月現在の）当社のアルゴリズムでは姿勢角の推定や初期姿勢角度計算に地磁気を利用しておりません．したがって，加速度（重力加速度）勾配から地面に対する傾きを補正できますが，補正するよりどころとしての方位情報が得られないため，例えるなら「暗闇の中でセンサを手で傾けたときのように，地面に対する傾きを知ることができても，どの方角を向いているかはわからない」状態であると想像してください．このため，実際に複数のセンサを異なる「方位」に向けて配置して計測開始しても，方位を知るすべがないので計測開始時に方位を統一させています．
たとえば，センサAのX軸を北向きに，センサBのX軸を西向きに配置したまま，計測を開始するとします．この際，実際の両センサのX軸に関しては９０度向きが異なっているはずですが，「計測開始時の姿勢角度のうち方位角」をそろえ，具体的には両ヨー角はゼロとなっています（クォータニオンのｚ軸成分をゼロとする）．
また，運動中も方位角に関しては補正ができないため，たとえゆっくり回転させるような姿勢角を計算する上で好条件な運動でも，「方位角はドリフトする（補正できない）」ことにも注意をしてください．
