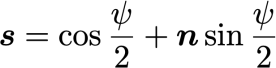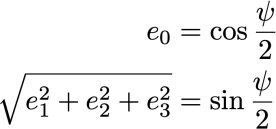クォータニオン3:ロドリゲスの式からクォータニオンへ
3次元空間の回転を表すロドリゲスの式が,複素数平面で2次元の回転を表現するオイラーの公式の幾何学的な拡張になっていることを「クォータニオン2:オイラーの公式からロドリゲスの式へ」で示しました.
ここでは,さらにこのロドリゲスの式と,オイラーパラメータ(単位クォータニオン)との関係について述べていきます.
オイラーパラメータ(単位クォータニオン)の導入
オイラーの公式によって表現される2次元回転は,同じ「指数関数」表現によるロドリゲスの式によって3次元回転へ拡張できることを述べました.オイラーの公式では,虚数を含む指数関数でしたが,3次元では[n x]という歪対称行列という行列に拡張されています.
そこで,次にオイラーの公式の右辺に着目します.右辺は複素数を用いて表現していますが,同様に3次元の回転でも,複素数の概念を3次元に拡張する必要があり,それが,クォータニオンに相当します.ただし,回転を表現するためには,ただのクォータニオンに大きさが1である球体の拘束があることに予め気をつけておく必要があります.
そこで,オイラーの公式
の虚数単位 i を3次元に拡張します.
この拡張は,オイラーパラメータ(単位クォータニオン) s を
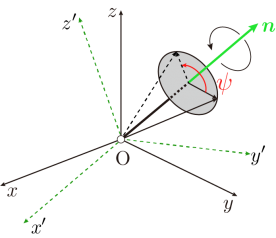
のように表すことで行います.ここで,オイラーの公式の虚数単位 i を3次元の単位ベクトル n に置き換え,この n は回転軸を表す単位ベクトルを表しています.また,回転角度がψの場合,この式ではψ/2を使用していることに注意をしてください.このことを除けば,オイラーの公式と非常に似ています.
ここで,複素数やクォータニオンの「+」の記号は単なる形式的な和の記号を意味し,スカラの構成パーツとベクトル成分の構成パーツの2つで表現していることを示しています.ただし,この和は交換則と分配則を満たし,実数と同様な計算が可能です.また,cosの項はスカラ部,第2項のsinの項はベクトル部と呼ばれます.
これは,複素数を単位クォータニオンへと幾何学的に拡張した表現ですが,異なる表現方法もあります.その名前のとおり,これをさらに4つのパラメータで表現する方法で,
虚数単位 i 以外に,j, k を新たに導入し,先ほどの回転軸 n に相当するベクトル部を3成分で表現し,
と4つのパラメータで表します.e0がスカラ部で回転量を表し,残りの3つの部分がベクトル部を示しています.
ここで,各鏡数単位は,
i*i = -1, j*j = -1, k*k = -1
のような虚数単位と同じ性質をそれぞれ持ち,さらに,
j*k= i, k*i = j, i*j = k, k*j = -i, i*k = -j, j*i = -k
という性質も満たします.
なお,これまで示した二つの表現方法は等価ですので,
という関係を満たしています.
また,オイラーパラメータは,そのベクトル部の座標系とその成分を意識し,さらに単位クォータニオンという側面から
と書かれることが多いようです.この場合,qwは回転量を表し,もしxyz座標系を使用した場合には,qx, qy, qzは回転軸のx, y, z成分を表しています.ただし,これらの値に単位はなく,回転角度ψはqw=cos ψ/2から,回転軸を示す単位ベクトルは[qx, qy, qz]のベクトルの単位ベクトルを計算する必要があることに注意してください.
以上をまとめると
のようになります.
オイラーパラメータで表すロドリゲスの式と回転行列
複素数による表現をオイラーパラメータに拡張することができましたので,最後に,ロドリゲスの式を使用して,回転行列をオイラーパラメータで表現すると,たとえば
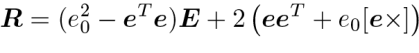
のように表すことができます.また,これをオイラーパラメータの成分で書くと
となります.
オイラーパラメータの特徴
3次元の姿勢や回転を表現する方法として,オイラー角が一般的でしたが,近年,ここで説明したオイラーパラメータを使用することが増えました.オイラーパラメータという名称はその由来と大きさに制約のない単なるクォータニオンと区別するために用いられている用語で,どちらかというとマイナーな名称です.単位クォータニオン(単位四元数)と呼ぶ方が,わかりやすいかもしれません.
さて,オイラー角は最小の3つのパラメータで表現できるという利点があるものの,3つの角度パラメータには幾何学的な意味はありません.これが,たびたび誤解を招きます.オイラー角はあくまでも姿勢回転行列を最小の3つのパラメータで表すための道具です.その3つの角度パラーメータに幾何学的意味はありません.特に解剖学的な角度(伸展・屈曲,回旋,内外転)などを表現するときには,条件によっては直感と大きく異なる角度が計算されることがあります.ご注意ください.
一方,オイラーパラメータはクォータニオンの大きさを1と拘束することで,回転を表現することができ,オイラー角ではできない,線形計算(クォータニオン積を使用した乗算等)が可能です.クォータニオン積を用いれば,異なるクォータニオンによる回転を,クォータニオンの積という形で表現できます.逆回転も計算できます.オイラー角を用いた場合は,いったん回転行列を計算する必要がありますが,クォータニオンは,クォータニオン同士の計算で閉じることができます.
また,一般には,特異点(ジンバルロックと呼ばれることがあるが,これはあくまでも,ジンバルという機構に生じる現象に過ぎない)を避けることができるという建前で,オイラーパラメータが導入されることが多いものの,角度や軸など直感的な表現方法ですし,一部の線形計算が可能など,多くの恩恵を得られます.
note記事
単位クォータニオンについてはnote記事「モーションにおける3次元回転」もご参照ください.