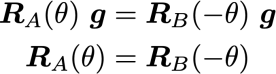ベクトルの回転と座標変換
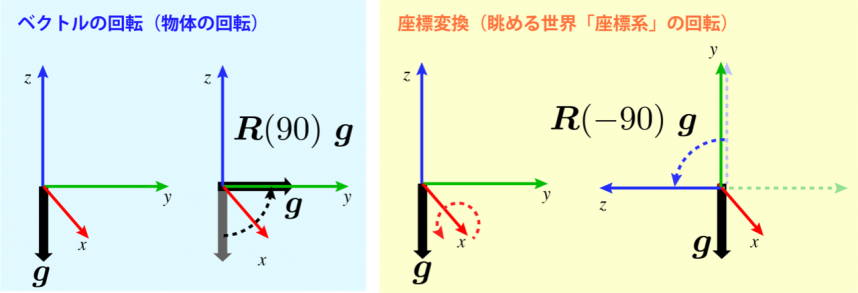
回転行列は,A「物体(に固定されたベクトル)を回転させる」場合と,B「物体(ベクトル)を眺める世界(座標系)を回転させる」場合とで,数学的な扱いが異なります.
「ベクトルを回転させる場合」「座標変換させる場合」の具体例
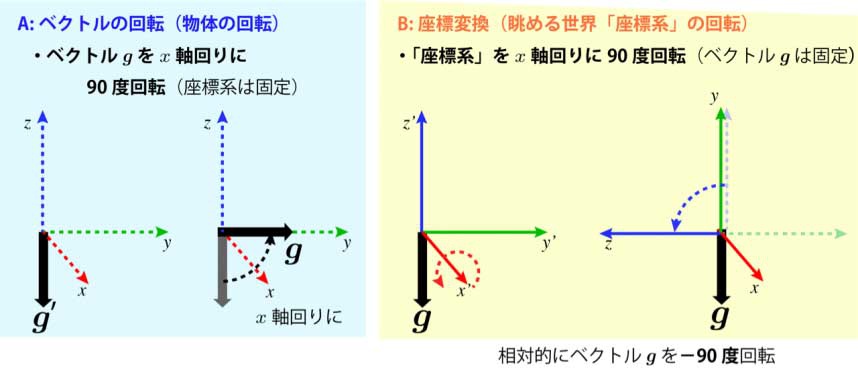
A)回転と,B)座標変換
この例からも,Aの物体に固定された「ベクトル」gをx軸回りに90度回転する場合と異なり,Bの物体を眺めている世界である「座標系」のほうをx軸回りに90度回転させることは,ベクトルgを相対的に反対方向に-90度,回転させることに相当します.
また,Aをベクトルの「回転」と呼び,Bをベクトルの「座標変換」と呼び,数学的にも区別されます.
そこで,ベクトルの回転を,x軸回りの回転角度θx(deg) の関数である回転行列R(θx)とベクトルgの乗積で表すと,Aの場合はR(90)gに相当し,Bの場合はR(-90)gで新しいベクトルを計算することに相当します.
すなわち,Aのベクトルの回転を行う行列と,Bのベクトルの座標変換を行う行列は,反対向き(逆回転)の関係であることがわかります.
数式での表現
そこで,改めてAの場合の回転行列をRA,Bの場合の座標変換行列をRBのように,それぞれ異なる行列RA, RB で区別して表すと,
Aの場合は行列RAでベクトルgを回転させ,Bの場合は行列RBでベクトルgを座標変換することになるので,
のように,それぞれの(A)回転と,(B)座標系変換を式で表すことができます.すると,(A)ベクトルgを90度回転することと,(B)ベクトルgを90度座標変換することは,
と,それぞれ書き表すことができますが,(A)回転と(B)座標変換では,ベクトルgを回転させる方向が反対向き,すなわち逆回転であることから,
のように,(90度の回転に限らず)一般的に上の式の関係が成り立ちます.すなわち回転行列RAと座標変換行列RBは反対向きの関係が成り立っています.
また,さらに,行列RAとRBは回転行列ですが,「回転行列」は数学の「直交行列」に相当し,その直交行列の数学的性質から,反対向きの回転が「転置行列」であることが知られていますので,
も成り立ちます.ここで,右上付きのTが行列の転置を意味し,R^Tは行列Rの転置行列を意味します.
回転行列(直交行列)の逆変換(逆回転)は転置行列
なお,回転行列R(θ)の反対向きの回転は,逆回転,すなわち回転行列の逆行列R(θ)^{-1}を乗算することに相当し,
も成り立ちます.
しかし,実際の計算では,決してわざわざ逆行列R^{-1}を計算することなく,「転置行列」R^Tを使用することで反対向きの回転や座標変換行列を計算しましょう.そのほうが計算が圧倒的に簡素です.
注意!
さて,実際の回転の問題を扱うときには,「何を(座標系かベクトルか)」,「どちら向きに」回転させるのかを具体的にイメージし,
・乗算すべき行列が「A回転行列か,B座標変換行列」か
・「どちら向きの回転(符号)」か
を,間違わないように気をつけましょう.
DSPモーションセンサの回転
なお,スポーツセンシング社のDSPモーションセンサは,絶対座標系に対するセンサの回転量をクォータニオンで出力します.
すなわち「絶対座標系(鉛直方向がZ軸)に対して」,「センサに固定された座標系の基底ベクトル(各XYZの軸の単位ベクトル)が,どの方法を向いているかを定めるクォータニオン」を出力します.
より具体的に述べますと,水平面に置いた(絶対座標系と一致している)状態の各センサの軸に固定された単位ベクトルex, ey, ezに対して,センサが出力するクォータニオンを用いて計算される回転行列(A)を乗算し,各ベクトルを回転させることで,新しいセンサの各軸の単位ベクトルex', ey', ez'を計算することができます.
複数センサを使用する際の注意
傾いた状態でモーションセンサの計測を開始すると,絶対座標系(鉛直上向きが,Z軸の正)に対するセンサの傾き(勾配)を反映した姿勢角を出力しますが,計測開始時のヨー角(方位角)が0となるクォータニオンを出力します.すなわち,計測開始した時点のヨー角,すなわち方位角を,0と初期化して,姿勢角を計算しています.
したがって,もし複数のセンサを使用し,出力されるクォータニオンを利用して,統一した座標系で各センサの姿勢角を計算する場合には,計測開始時に各センサの傾き(Z軸の向き)が異なっていてもかまいませんが,センサの方位は揃えた状態(センサを鉛直上方から見て,各X,Y軸の向きが平行になるように)で計測開始を行ってください.