紙スポ・オンラインショップがオープンしました
紙と鉛筆ではじめるゲーム分析シート「紙スポ」のオンラインショップがオープンしました
紙スポとは、「紙で進めるスポーツ分析」の略語です。
従来は大きな投資が必要なスポーツの分析を、様々な入力フォーマットを用意することで、
効率的にデータの記録、集計、フィードバックを行います。
加速度センサの基礎
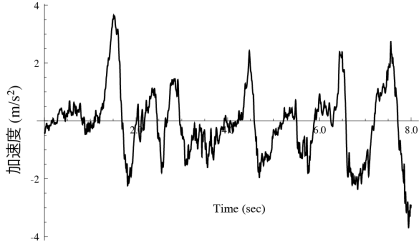
モーションセンサを構成する加速度センサについて解説します.自由に運動している物体に加速度センサを装着して運動を計測した例が,上の図の加速度です.同じ加速度信号でも,この信号をどの座標系から観察した加速度と捉えるかで,この信号の意味が変わってきます.
では,加速度とは何でしょう?速度は,位置の変化率,すなわち単位時間あたりにどの程度位置(変位)が変化しているか観察した量が速度です.当たり前ですが位置がどんどんずれると速度を持つことになり,位置が変わらないと速度がゼロです.感覚的にもこの物理量はわかりやすいと思います.加速度は,さらにこの速度の単位時間あたりの変化率を指します.同じように速度が変化すると(増加したり,減少したりすると),加速度が生じます.
速度の単位は単位時間あたりの位置の変化量ですから[m/s]です.ですから,加速度の単位はさらにもう一度時間で割るので[m/s^2]です.しかし,これは一般的な科学で用いられる SI単位で,加速度センサは通常重力加速度[g]を単位としています.つまり,地球が物体を引張る引力を基準にした加速度で,1[g]はおおよそ9.8[m/s^2]です.重力加速度は実際には場所によって異なってしまいますが,ほとんどセンサの誤差範囲内です.国土地理院のデータによると東京の重力加速度は9.798[m/s^2]ぐらいです.北海道ですと9.805[m/s^2]です.地域によって結構違いがありますが,加速度センサの値に9.8倍した値を加速度として計算して問題ないでしょう.
実は加速度センサは力センサである
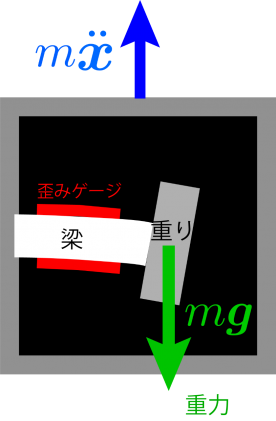
加速度センサの内部は各社で異なりますが,多くのタイプのセンサでは実は力センサが内蔵されていると考えてください.実際のセンサの内部構造と異なりますが,歪みゲージ型の加速度センサと同様に,梁に作用する歪みを測っていると考えるとわかりやすいです.
図に示したように加速度センサには梁とその先に重りがついていると考えてください.梁には歪みゲージが貼ってあります.これと同等な構造が一般的な加速度センサに入っていると考えてください.加速度センサはこの梁のたわみを測っています.すると,このたわみ変形は,重りに作用する力によって変化します.つまり,静止していても重力を含んだ力を計測しています.この点にご注意ください.
加速度センサに作用している力を中の重りの質量mで割ると,加速度が計算されます.この値を加速度センサが算出していると考えてください.ですから加速度センサは実は力センサなのです.力センサなので,動いていないのに重力加速度も測定しています.センサを静止した状態である向きでキャリブレーションして,この重力加速度をリセットしたつもりでも,向きが変われば,他の軸にこの重力加速度は含まれています.重力加速度が,必ず含まれていることにご注意ください.
加速度信号の符号(注意点)
スポーツコーチングカムのレンタル
「ゲーム分析にタギングを行いたい」「映像サポートの効率を高めたい」お客様に多くのご高評いただいている「スポーツコーチングカム」のレンタルサービスです。
レンタルプラン
レンタル期間に応じた幾つかのプランをご用意しております。
スーパーショートプラン(~14日)
15,000
26,000:(バッテリーパック付)
ショートプラン(1ヶ月~3ヶ月)
20,000/月
25,000/月:(バッテリーパック付)
ミドルプラン(1ヶ月~5ヶ月)
14,000/月
22,000/月:(バッテリーパック付)
ロングプラン(6ヶ月~1年)
13,000/月
19,000/月:(バッテリーパック付)
※返送料はお客様ご負担となります。
レンタルのお申込み
お問い合わせフォームより、ご連絡下さい。
【プレスリリース】スポーツコーチングカメラシステムが近接無線技術TransferJet™に対応
スポーツコーチングカメラシステムが近接無線技術TransferJet™に対応
~スポーツコーチング用アプリケーションソフト「Sports Coaching VIEWER Ver.2.5」をリリース~
株式会社スポーツセンシングは、株式会社JVCケンウッド(本社:神奈川県横浜市、代表取締役社長:辻孝夫、以下JVCケンウッド)と共同開発したスポーツコーチングカメラシステムが、近接無線技術TransferJet™に新たに対応したことをお知らせします。当社が開発したスポーツコーチング用アプリケーションソフト「Sports Coaching VIEWER」※1において、株式会社東芝(本社:東京都港区、代表執行役社長:綱川智、以下東芝)製のTransferJet™搭載SDHCメモリカードおよびTransferJet™対応アダプタを使用出来る新バージョン(Ver2.5)をリリース致します。
企画背景と特長
当社の無線技術とJVCケンウッドのビデオカメラ技術を融合して共同開発したスポーツコーチングカメラシステム(2014年10月発売)は、撮影しながらイベント情報を記録できる“タギング”機能を搭載し、必要なシーンへすばやくアクセスすることができる、映像を用いた分析ソリューションとして発売以来、トップアスリートの育成・強化など多くのスポーツの現場で活用されてきました。
しかしこれまで、スポーツコーチング本カメラシステムで撮影した映像は、一旦パソコンへ取り込み、映像分析アプリケーションでの編集作業が必要であり、競技中の選手にその場でフィードバックするにはタイムラグが生じていました。
今回、東芝製の近接無線技術TransferJet™を搭載したアダプタおよびSDHCメモリカードに対応することで、当社のスポーツコーチング用アプリケーションソフト※1「Sports Coaching VIEWER Ver.2.5」を用い、スポーツコーチング本カメラシステムの映像にタギング情報を記録したファイルをタブレット端末※1に無線転送することを可能にしました。これにより、映像を撮影した本カメラシステムにタブレットを近づけるだけでタギング情報の付加された映像が自動で無線転送されるため、トレーニングや試合中における映像を用いたフィードバックの大幅なスピードアップを実現します。また、競技者・指導者・分析スタッフが機器の難しい操作を習熟する必要がなくなり、さらなる競技力向上に貢献します。
当社は、映像を用いたスポーツコーチングソリューションがシンプルに構築できる本システムをトップアスリート層だけでなく、各種スポーツ入門層や小規模サークルなどに向けて幅広く提案していきます
※1:iPad(iOS9.0以降)に対応。