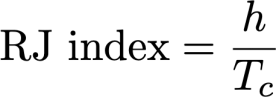![]()
トランポリンと跳躍競技におけるインピーダンスマッチング
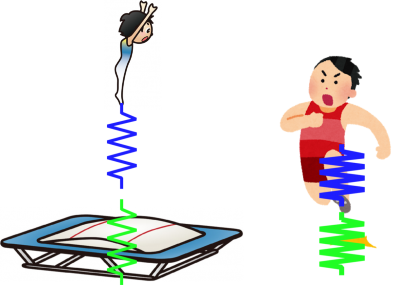
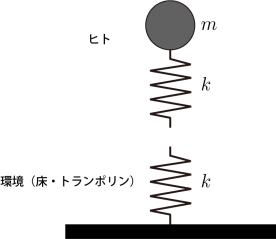
トランポリン競技では,身体をトランポリンのバネ特性にあわせるような力発揮を行い,「あたかも」同程度の硬さのバネとして振る舞うことでより高く跳躍することができます.
一方,陸上競技の短距離走や跳躍競技などでは床が硬いため,トランポリン競技などと比較すると身体を「あたかも」より硬いバネのように振る舞わせ,床面との間に高い反発力を生み出すことで,より高い競技能力を達成していると考えられています.他にもバスケットボールやサッカーなどにおける方向転換などでは,「短時間で力やパワーを発揮する能力」が必要とされ,ここでは「高反発特性」と形容することにします.
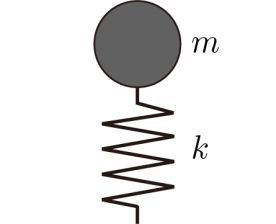
これは物理的には共振や機械的インピーダンスマッチングと同じ原理で説明することができます.たとえば,スーパーボールが床面の硬さに見合った高い弾性特性をもっているために,高反発することと同じ原理です.すなわち,競技力を向上させるために,トランポリンや床などの「環境の硬さ(機械インピーダンス)」に応じて,「身体の硬さ」を同程度に「共振(マッチング)・整合」させる,最適な力学原理に自然と従うように,ヒトはトレーニングによって高い跳躍力を獲得していると言えます.
したがって,この「高反発特性」は機械的なインピーダンスマッチングという適応から,言い換えるなら「硬い床面という環境に適応して,身体が大きな反力を獲得する」という競技特性から必要とされている能力と言えます.
なお,冒頭「あたかも」と強調したのは,身体全体がそのような固有の弾性特性を有しているわけではなく,全身の制御を行っている結果,「あたかも」見かけ上そのような弾性特性を実現しているだけで,その特性は筋肉固有の物理的特性ではありません.ただし,特に大きな反力を必要とするような制御を実現するためには,トレーニング等によって獲得された高い筋骨格系の能力が不可欠です.
![]()
同じバネ特性による共振(機械インピーダンス整合)
連続リバウンドジャンプとRJ指数
トランポリンのようなバネよりもさらに硬い床面に対して,短時間で高反発するように力やパワーを発揮する「高反発特性」は,一般には連続リバウンドジャンプの計測によって調べられるRJ指数(リバウンドジャンプ・インデックス)で数値化できます.
連続リバウンドジャンプとは「できるだけ短い接地時間で高く跳び上がる」動作を連続して行う動作です.国立スポーツ科学センター(JISS)で行われている標準的な計測では,5回連続してジャンプを繰り返します.
陸上の跳躍競技などの高反発特性を有する選手の連続リバウンドジャンプでは,一般に「跳躍高が高く」,「接地時間が短い」傾向が顕著です.そこで,この「跳躍高」と「接地時間」の比であるRJ指数を計算することで,被験者の下肢や体幹の「短時間で発揮するパワー発揮能力」(高反発特性)を調べることができ,国内では普及した測定方法と指標となっています.幸い,国立スポーツ科学センター(JISS)でも,エリートアスリートの体力測定の測定項目として公開されていますので,一流選手のデータと比較することも可能です(参考資料:フィットネスチェックハンドブック―体力測定に基づいたアスリートへの科学的支援―,ハイパフォーマンスセンター:フィットネスチェックマニュアル).
そこで,次にマットスイッチを使用した,パワー発揮能力の評価方法について具体的にご説明します.
連続リバウンドジャンプ
ここでは,国立スポーツ科学センターの計測方法をご紹介します(ハイパフォーマンスセンター:フィットネスチェックマニュアル).
ウォーミングアップ
マットスイッチによるRJ(リバウンドジャンプ)指数の測定 の続きを読む