加速度センサの基礎
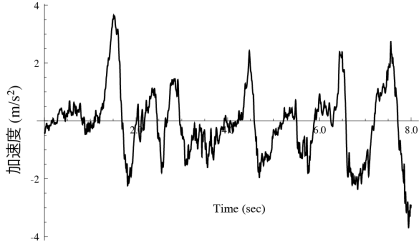
モーションセンサを構成する加速度センサについて解説します.自由に運動している物体に加速度センサを装着して運動を計測した例が,上の図の加速度です.同じ加速度信号でも,この信号をどの座標系から観察した加速度と捉えるかで,この信号の意味が変わってきます.
では,加速度とは何でしょう?速度は,位置の変化率,すなわち単位時間あたりにどの程度位置(変位)が変化しているか観察した量が速度です.当たり前ですが位置がどんどんずれると速度を持つことになり,位置が変わらないと速度がゼロです.感覚的にもこの物理量はわかりやすいと思います.加速度は,さらにこの速度の単位時間あたりの変化率を指します.同じように速度が変化すると(増加したり,減少したりすると),加速度が生じます.
速度の単位は単位時間あたりの位置の変化量ですから[m/s]です.ですから,加速度の単位はさらにもう一度時間で割るので[m/s^2]です.しかし,これは一般的な科学で用いられる SI単位で,加速度センサは通常重力加速度[g]を単位としています.つまり,地球が物体を引張る引力を基準にした加速度で,1[g]はおおよそ9.8[m/s^2]です.重力加速度は実際には場所によって異なってしまいますが,ほとんどセンサの誤差範囲内です.国土地理院のデータによると東京の重力加速度は9.798[m/s^2]ぐらいです.北海道ですと9.805[m/s^2]です.地域によって結構違いがありますが,加速度センサの値に9.8倍した値を加速度として計算して問題ないでしょう.
実は加速度センサは力センサである
加速度センサの内部は各社で異なりますが,多くのタイプのセンサでは実は力センサが内蔵されていると考えてください.実際のセンサの内部構造と異なりますが,歪みゲージ型の加速度センサと同様に,梁に作用する歪みを測っていると考えるとわかりやすいです.
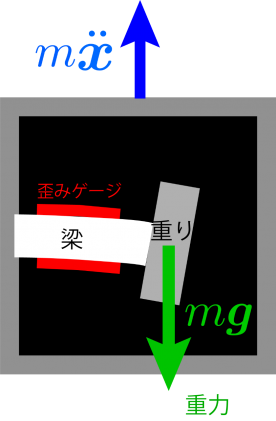
図に示したように加速度センサには梁とその先に重りがついていると考えてください.梁には歪みゲージが貼ってあります.これと同等な構造が一般的な加速度センサに入っていると考えてください.加速度センサはこの梁のたわみを測っています.すると,このたわみ変形は,重りに作用する力によって変化します.つまり,静止していても重力を含んだ力を計測しています.この点にご注意ください.
加速度センサに作用している力を中の重りの質量mで割ると,加速度が計算されます.この値を加速度センサが算出していると考えてください.ですから加速度センサは実は力センサなのです.力センサなので,動いていないのに重力加速度も測定しています.センサを静止した状態である向きでキャリブレーションして,この重力加速度をリセットしたつもりでも,向きが変われば,他の軸にこの重力加速度は含まれています.重力加速度が,必ず含まれていることにご注意ください.