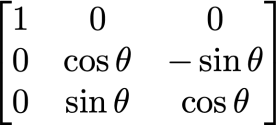オイラー角による姿勢表現
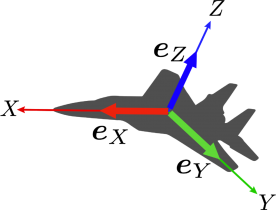
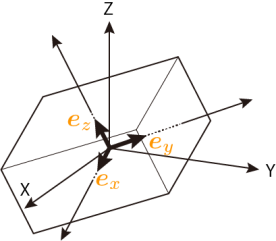
物体の3次元における姿勢は,3つの直交する単位ベクトル(大きさが1のベクトル)で表現します.
これらは,直交座標系の軸上に配置された,単位ベクトルとも言えます.
この単位ベクトルをeX, eY, eZとすると,この単位ベクトルを並べたもの(基底)が回転行列Rとなります.つまり,姿勢は回転行列で表現します.これが基本となります.
回転行列というと
のような三角関数で表した行列を連想する方も多いと思います.回転行列は数学的には直交行列の性質を満たし,上記のX軸回りの回転行列も,大きさが1で直交する単位ベクトルを並べたものとなっています.
このように,3つの直交する単位ベクトルを構築して,それらを並べれば回転行列となります.したがって回転行列を計算するために,必ずしも角度を計算する必要はありません.