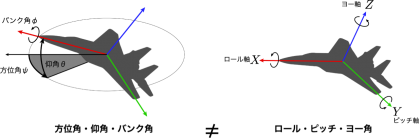
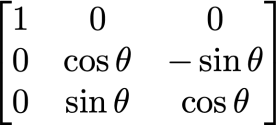オイラー角による姿勢表現

オイラー角による物体の姿勢表現

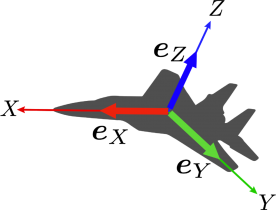
物体の3次元における姿勢は，3つの直交する単位ベクトル（大きさが1のベクトル）で表現します．
これらは，直交座標系の軸上に配置された，単位ベクトルとも言えます．
この単位ベクトルをeX, eY, eZとすると，この単位ベクトルを並べたもの（基底）が回転行列Rとなります．つまり，姿勢は回転行列で表現します．これが基本となります．

回転行列というと

のような三角関数で表した行列を連想する方も多いと思います．回転行列は数学的には直交行列の性質を満たし，上記のＸ軸回りの回転行列も，大きさが1で直交する単位ベクトルを並べたものとなっています．

このように，3つの直交する単位ベクトルを構築して，それらを並べれば回転行列となります．したがって回転行列を計算するために，必ずしも角度を計算する必要はありません．

オイラー角は，あくまでも物体の姿勢を表現する方法の一つです．
また，角度で姿勢を表現しますが，たとえば，物体の傾きや軸回転を表す方法ではありません．

オイラー角の表現方法

オイラー角は，各座標軸まわりの，3つの回転の組み合わせ　と　順番　によって姿勢を表します．
2番目，3番目の回転は，一つ前の回転後の新しい座標軸における新しい軸まわりの回転となります．つまり，オイラー角は軸の選択とその順番に依存する定義です．
姿勢を表す回転行列は9つのパラメータで表現されていましたが，オイラー角は，回転順序という拘束と3つの角度パラメータで定義される，姿勢表現のための道具です．
このことからも，回転や姿勢の変化は，そもそも3つのパラメータだけで表現できるということもわかります．

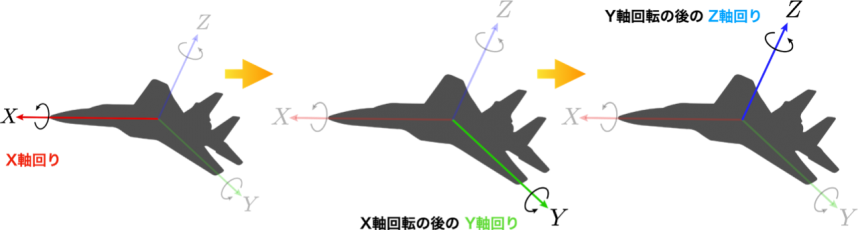
例：XYZオイラー角

上記図のように，X軸回りの回転　→　回転後のY軸回りに回転　→　回転後のZ軸回りに回転　の順番で回転させる角度をXYZオイラー角と呼びます．

オイラー角の組み合わせ（12種類）

このように，回転順序がオイラー角を決めますが，同じ角度を2度回転させても構いません．ただし，同じ回転は続いてはいけません．すると，その組み合わせは，下記の12通りになります．
姿勢はどのオイラー角を用いても一意に決まりますが，12種類の角度の組み合わせがあり，角度値もそれぞれ異なります．このように，オイラー角の3つのパラメータのそれぞれには特に幾何学的，物理的な意味はありません．あくまでも，姿勢を表すための道具です．

3軸が全て異なる回転

　XYZ, XZY, YZX, YXZ, ZXY, ZYX

最初と最後の軸回転を繰り返す回転

　XZX, XYX, YZY, YXY, ZXZ, ZYZ

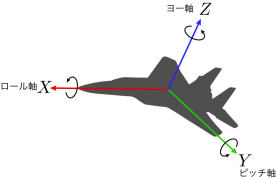
ロール，ピッチ，ヨー角

このうち，ZYXオイラー角は，特別にロール・ピッチ・ヨー角と呼ばれることがあります．
これらは，紛らわしい名称で，ローリング角がバンク角，ピッチング角が上昇角，ヨー角が方位角のような連想をしてしまいますが，ロール角，ピッチ角，ヨー角は，各軸回転角度を反映していません．繰り返しになってしまいますが，ロール，ピッチ，ヨー角に限らず，物体に固定された軸のまわりの回転角度とは一致しません．

オイラー角はあくまでも姿勢を表現するための方法

オイラー角は，方位角・仰角・バンク角とも一致しません．

また，オイラー角は，身体部位の姿勢表現に用いられることもありますが，各回転角度は，解剖学的な角度を反映しません．
そもそも，解剖学的に定義された「外転」などは数学的に定義された角度ではなく，あいまいな角度定義ですが，これまで述べた理由から，オイラー角は解剖学的な角度を表現することに対してもあまり適してはいません．

オイラー角の数理的な概要については，「姿勢角度の算出」をご覧ください．

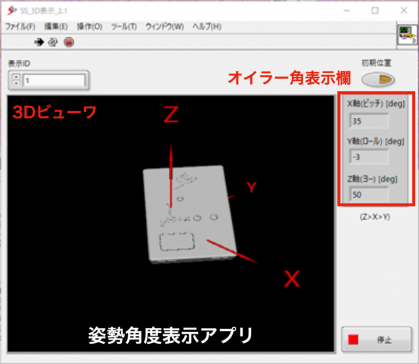
姿勢角度表示アプリ

姿勢角度表示アプリでは，リアルタイムでセンサを動かしながら，3Ｄビューによるグラフィックスと，ZXYオイラー角の数値を，センサを動かしながら確認することができます．

姿勢角度を表現する他の方法

オイラー角以外の姿勢角度を表す方法として，代表的な方法として，クォータニオン（四元数）があります．そのなかでも大きさが1の単位クォータニオンは，姿勢の変化を，回転軸（ベクトル）と回転を表すスカラーの合計4つのパラメータで表す方法です．回転軸ベクトルなので成分に分解することもできますから，直感的でわかりやすく，クォータニオンの演算も線形に行うことができるなどの，多くの利点があります．オイラー角と比較して，パラメータが一つ多く，冗長ですが優れた姿勢や回転の表現方法です．

オイラー角による姿勢表現