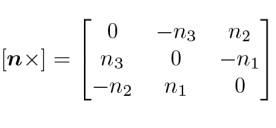ロドリゲスの式
オイラーの定理
回転行列 R は剛体の姿勢を表すとします.すると,Ra のように,行列 R はベクトル a の回転の役割も果たします.この回転を,1 本の固定軸 n まわりに角度 ψ だけまわす 1 回転で表現することができます.つまり,R に対して必ずそのような 1 本の固定軸が存在することが知られています.これはオイラーの定理と呼ばれています.
そのような行列Rによるベクトルaの回転は式で
のように表します.
ロドリゲスの式
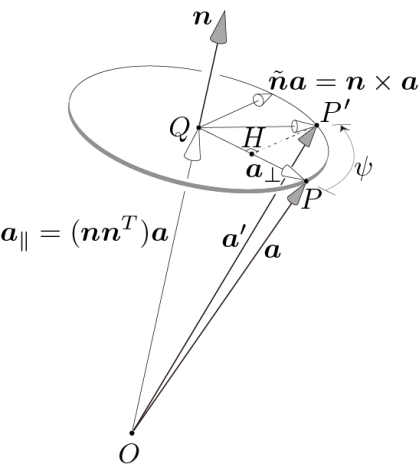
次に,図に示すように,ベクトル a を,単位ベクトル n 方向の直線まわりに角度 ψ だけ回転させることを考え,回転後のそのベクトルを a′ とします.こ れらのベクトルはどこにあっても議論が可能ですが,ここでは説明の便宜上,全て のベクトルの始点が点 O に一致していると仮定します.
すると回転行列Rは
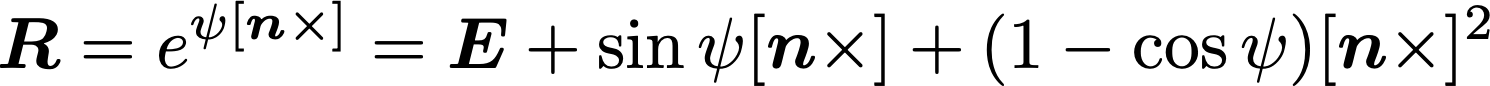
のように表すことができます.これをロドリゲスの式と呼びます.ここで,E は3次の単位行列で,
は,ベクトルnの外積を表す歪対称行列です.これをかけることで,外積と同じ役割を果たします.ここでは証明を省きますが,2番目の式のように,オイラーの公式同様に,回転が指数関数で表現できることだけ付記しておきます.2次元平面の回転を表すオイラーの公式と,3次元の回転を表現するロドリゲスの式の類似性は「オイラーの公式からロドリゲスの式へ」をご覧ください.
つまり,このR使って,ベクトル a を軸 n まわりに角度 ψ だけ,回転行列 R によって回転させて,ベクトルa'に移動することになります.
DSPを搭載しセンサ内部で柔軟な演算を行える新機軸の無線センサ
スタジオで計測いただくことができます
約100㎡(10m x 10m)のスペースがある計測スタジオをレンタルいただく事で、DSP9軸ワイヤレスモーションセンサ等を使用して運動計測、身体計測を行うことができます。
お問い合わせ
製品についてのご質問などお気軽にお問い合わせ下さい。